2018届淄博市高考理科数学模拟试卷及答案
备战高考理科数学,我们需要多做一些高考理科数学模拟试卷来进行查漏补缺,分重难点进行复习,下面是小编为大家精心推荐的2018届淄博市高考理科数学模拟试卷,希望能够对您有所帮助。
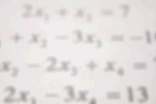
2018届淄博市高考理科数学模拟试卷题目
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={x|x2﹣4x<0},B={x|x
A.(0,4] B.(﹣∞,4) C.[4,+∞) D.(4,+∞)
2.欧拉公式eix=cosx+isinx (i为虚数单位)是瑞士数学家欧拉发明的,将指数的定义域扩大到复数集,建立了三角函数和指数函数的联系,被誉为“数学中的天桥”.根据欧拉公式可知,e 表示的复数的模为( )
A. B.1 C. D.
3.已知某几何体的三视图如图所示,则该几何体的体积是( )
A.100 B.82 C.96 D.112
4.已知函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )
A.函数f(x)的最小正周期为
B.直线x=﹣ 是函数f(x)图象的一条对称轴
C.函数f(x)在区间[﹣ , ]上单调递增
D.将函数f(x)的图象向左平移 个单位,得到函数g(x)的图象,则g(x)=2sin2x
5.对于四面体A﹣BCD,有以下命题:①若AB=AC=AD,则AB,AC,AD与底面所成的角相等;②若AB⊥CD,AC⊥BD,则点A在底面BCD内的射影是△BCD的内心;③四面体A﹣BCD的四个面中最多有四个直角三角形;④若四面体A﹣BCD的6条棱长都为1,则它的内切球的表面积为 .其中正确的命题是( )
A.①③ B.③④ C.①②③ D.①③④
6.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )
A.21 B.22 C.23 D.24
7.若数列{an}是正项数列,且 + +…+ =n2+n,则a1+ +…+ 等于( )
A.2n2+2n B.n2+2n C.2n2+n D.2(n2+2n)
8.某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )
A.18种 B.24种 C.36种 D.48种
9.命题p:已知数列{an}为等比数列,且满足a3•a6= dx,则logπa4+logπa5= ;命题q:“∀x∈R,sinx≠1”的否定是“∃x∈R,sinx=1”.则下列四个命题:¬p∨¬q、p∧q、¬p∧q、p∧¬q中,正确命题的个数为( )
A.4 B.3 C.2 D.1
10.已知定义在R上的偶函数f(x),满足f(x+4)=f(x),且x∈[0,2]时,f(x)=sinπx+2|sinπx|,则方程f(x)﹣|lgx|=0在区间[0,10]上根的个数是( )
A.17 B.18 C.19 D.20
11.抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线 ﹣ =1(a>0,b>0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )
A. B.2 C. D. +1
12.已知函数f(x)=xlnx+3x﹣2,射线l:y=kx﹣k(x≥1).若射线l恒在函数y=f(x)图象的下方,则整数k的最大值为( )
A.4 B.5 C.6 D.7
二、填空题( x﹣1)(2x﹣ )6的展开式中x的系数为 .(用数字作答)
14.若实数x,y满足不等式组 ,则 的最小值为 .
15.在[﹣2,2]上随机抽取两个实数a,b,则事件“直线x+y=1与圆(x﹣a)2+(y﹣b)2=2相交”发生的概率为 .
16.在平面内,定点A,B,C,D满足| |=| |=| |=2, • = • = • =0,动点P,M满足| |=1, = ,则| |2的最大值为 .
三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,已知3(b2+c2)=3a2+2bc.
(Ⅰ)若 ,求tanC的大小;
(Ⅱ)若a=2,△ABC的面积 ,且b>c,求b,c.
18.(12分)质检部门从某超市销售的甲、乙两种食用油中分划随机抽取100桶检测某项质量指标,由检测结果得到如图的频率分布直方图:
(I)写出频率分布直方图(甲)中a的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为s12,s22,试比较s12,s22的大小(只要求写出答案);
(Ⅱ)估计在甲、乙两种食用油中随机抽取1捅,恰有一个桶的质量指标大于20,且另一个不大于20的概率;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值Z服从正态分布N(μ,δ2).其中μ近似为样本平均数 ,δ2近似为样本方差s22,设X表示从乙种食用油中随机抽取lO桶,其质量指标值位于(14.55,38.45)的桶数,求X的散学期望.
注:①同一组数据用该区问的中点值作代表,计算得s2= ≈11.95;
②若Z﹣N(μ,δ2),则P(μ﹣δ
19.(12分)如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE= CD,M是线段AE上的动点.
(Ⅰ)试确定点M的位置,使AC∥平面DMF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
20.(12分)已知△ABC中,角A,B,C所对的边分别是a,b,c,且点A(﹣1,0),B(1,0),动点C满足 =λ(λ为常数且λ>1),动点C的轨迹为曲线E.
(Ⅰ)试求曲线E的方程;
(Ⅱ)当λ= 时,过定点B(1,0)的直线与曲线E交于P,Q两点,N是曲线E上不同于P,Q的动点,试求△NPQ面积的最大值.
21.(12分)已知函数f(x)=exsinx﹣cosx,g(x)=xcosx﹣ ex,其中e是自然对数的底数.
(1)判断函数y=f(x)在(0, )内的零点的个数,并说明理由;
(2)∀x1∈[0, ],∃x2∈[0, ],使得f(x1)+g(x2)≥m成立,试求实数m的取值范围;
(3)若x>﹣1,求证:f(x)﹣g(x)>0.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.(10分)在平面直角坐标系xOy中,曲线C1: (α是参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2:ρcosθ﹣3=0.点P是曲线C1上的动点.
(1)求点P到曲线C2的距离的最大值;
(2)若曲线C3:θ= 交曲线C1于A,B两点,求△ABC1的面积.
[选修4-5:不等式选讲]
23.已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
2018届淄博市高考理科数学模拟试卷答案
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={x|x2﹣4x<0},B={x|x
A.(0,4] B.(﹣∞,4) C.[4,+∞) D.(4,+∞)
【考点】18:集合的包含关系判断及应用.
【分析】利用一元二次不等式可化简集合A,再利用A⊆B即可得出.
【解答】解:对于集合A={x|x2﹣4x<0},由x2﹣4x<0,解得0
又B={x|x
∵A⊆B,
∴a≥4.
∴实数a的取值范围是a≥4.
故选C.
【点评】本题考查了一元二次不等式的解法、集合之间的关系,属于基础题.
2.欧拉公式eix=cosx+isinx (i为虚数单位)是瑞士数学家欧拉发明的,将指数的定义域扩大到复数集,建立了三角函数和指数函数的联系,被誉为“数学中的天桥”.根据欧拉公式可知,e 表示的复数的模为( )
A. B.1 C. D.
【考点】A8:复数求模.
【分析】直接由题意可得 =cos +isin ,再由复数模的计算公式得答案.
【解答】解:由题意, =cos +isin ,
∴e 表示的复数的模为 .
故选:B.
【点评】本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.
3.已知某几何体的三视图如图所示,则该几何体的体积是( )
A.100 B.82 C.96 D.112
【考点】L!:由三视图求面积、体积.
【分析】由已知中的三视图可得:该几何体是一个长方体切去一个三棱锥得到的组合体,分别计算长方体和棱锥的体积,相减可得答案.
【解答】解:由已知中的三视图可得:该几何体是一个长方体切去一个三棱锥得到的组合体,
长方体的体积为:6×6×3=108,
棱锥的体积为: ×4×3×4=8,
故组合体的体积V=108﹣8=100,
故选:A.
【点评】本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度中档.
4.已知函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )
A.函数f(x)的最小正周期为
B.直线x=﹣ 是函数f(x)图象的一条对称轴
C.函数f(x)在区间[﹣ , ]上单调递增
D.将函数f(x)的图象向左平移 个单位,得到函数g(x)的图象,则g(x)=2sin2x
【考点】H2:正弦函数的图象.
【分析】先求出函数的解析式,再进行判断,即可得出结论.
【解答】解:根据函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<π)的部分图象,
可得A=2,图象的一条对称轴方程为x= = ,一个对称中心为为( ,0),
∴ = = ,∴T= ,∴ω=2,
代入( ,2)可得2=2sin(2× +φ),∵|φ|<π,∴φ=﹣ ,
∴f(x)=2sin(2x﹣ ),将函数f(x)的图象向左平移 个单位,可得g(x)=2sin[2(x+ )﹣ ]=2sin2x,
故选:D.
【点评】本题考查三角函数的图象与性质,考查学生的计算能力,确定函数的解析式是关键.
5.对于四面体A﹣BCD,有以下命题:①若AB=AC=AD,则AB,AC,AD与底面所成的角相等;②若AB⊥CD,AC⊥BD,则点A在底面BCD内的射影是△BCD的内心;③四面体A﹣BCD的四个面中最多有四个直角三角形;④若四面体A﹣BCD的6条棱长都为1,则它的内切球的表面积为 .其中正确的命题是( )
A.①③ B.③④ C.①②③ D.①③④
【考点】2K:命题的真假判断与应用.
【分析】对于①,根据线面角的定义即可判断;
对于②,根据三垂线定理的逆定理可知,O是△BCD的垂心,
对于③在正方体中,找出满足题意的四面体,即可得到直角三角形的个数,
对于④作出正四面体的图形,球的球心位置,说明OE是内切球的半径,利用直角三角形,逐步求出内切球的表面积.
【解答】解:对于①,因为AB=AC=AD,设点A在平面BCD内的射影是O,因为sin∠ABO= ,sin∠ACO= ,sin∠ADO= ,所以sin∠ABO=sin∠ACO=sin∠ADO,
则AB,AC,AD与底面所成的角相等;故①正确;
对于②设点A在平面BCD内的射影是O,则OB是AB在平面BCD内的射影,因为AB⊥CD,根据三垂线定理的逆定理可知:CD⊥OB 同理可证BD⊥OC,所以O是△BCD的垂心,故②不正确;
对于③:如图:直接三角形的直角顶点已经标出,直角三角形的个数是4.故③正确
对于④,如图O为正四面体ABCD的内切球的球心,正四面体的棱长为:1;
所以OE为内切球的半径,BF=AF= ,BE= ,
所以AE= = ,
因为BO2﹣OE2=BE2,
所以( ﹣OE)2﹣OE2=( )2,
所以OE= ,
所以球的表面积为:4π•OE2= ,故④正确.
故选D.
【点评】本题考查命题的真假判断与应用,综合考查了线面、面面垂直的判断与性质,考查了学生的空间想象能力,是中档题.
6.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )
A.21 B.22 C.23 D.24
【考点】EF:程序框图.
【分析】该程序框图的作用是求被3和5除后的余数为2的数,根据所给的选项,得出结论.
【解答】解:该程序框图的作用是求被3除后的余数为2,被5除后的余数为3的数,
在所给的选项中,满足被3除后的余数为2,被5除后的余数为3的数只有23,
故选:C.
【点评】本题主要考查程序框图的应用,属于基础题.
7.若数列{an}是正项数列,且 + +…+ =n2+n,则a1+ +…+ 等于( )
A.2n2+2n B.n2+2n C.2n2+n D.2(n2+2n)
【考点】8H:数列递推式.
【分析】利用数列递推关系可得an,再利用等差数列的求和公式即可得出.
【解答】解:∵ + +…+ =n2+n,∴n=1时, =2,解得a1=4.
n≥2时, + +…+ =(n﹣1)2+n﹣1,
相减可得: =2n,∴an=4n2.n=1时也成立.
∴ =4n.
则a1+ +…+ =4(1+2+…+n)=4× =2n2+2n.
故选:A.
【点评】本题考查了等差数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.
8.某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )
A.18种 B.24种 C.36种 D.48种
【考点】D8:排列、组合的实际应用.
【分析】根据题意,分2种情况讨论:①、A户家庭的孪生姐妹在甲车上,甲车上剩下两个要来自不同的家庭,②、A户家庭的孪生姐妹不在甲车上,每种情况下分析乘坐人员的情况,由排列、组合数公式计算可得其乘坐方式的数目,由分类计数原理计算可得答案.
【解答】解:根据题意,分2种情况讨论:
①、A户家庭的孪生姐妹在甲车上,甲车上剩下两个要来自不同的家庭,
可以在剩下的三个家庭中任选2个,再从每个家庭的2个小孩中任选一个,来乘坐甲车,
有C32×C21×C21=12种乘坐方式;
②、A户家庭的孪生姐妹不在甲车上,
需要在剩下的三个家庭中任选1个,让其2个小孩都在甲车上,
对于剩余的2个家庭,从每个家庭的2个小孩中任选一个,来乘坐甲车,
有C31×C21×C21=12种乘坐方式;
则共有12+12=24种乘坐方式;
故选:B.
【点评】本题考查排列、组合的应用,涉及分类计数原理的应用,关键是依据题意,分析“乘坐甲车的4名小孩恰有2名来自于同一个家庭”的可能情况.
9.命题p:已知数列{an}为等比数列,且满足a3•a6= dx,则logπa4+logπa5= ;命题q:“∀x∈R,sinx≠1”的否定是“∃x∈R,sinx=1”.则下列四个命题:¬p∨¬q、p∧q、¬p∧q、p∧¬q中,正确命题的个数为( )
A.4 B.3 C.2 D.1
【考点】2E:复合命题的真假.
【分析】利用微积分基本定理与等比数列的性质即可判断出命题p的真假;利用复合命题真假的判定方法即可判断出命题q的真假.再利用复合命题真假的判定方法即可判断出真假.
【解答】解:命题p:已知数列{an}为等比数列,且满足a3•a6= dx= ×π×22=π,则logπa4+logπa5=logπ(a4a5)=logπ(a3a6)=logππ=1≠ ,因此是假命题;
命题q:“∀x∈R,sinx≠1”的否定是“∃x∈R,sinx=1”,是真命题.
则下列四个命题:¬p∨¬q、p∧q、¬p∧q、p∧¬q中,只有¬p∨¬q、¬p∧q是真命题.
正确命题的个数是2.
故选:C.
【点评】本题考查了微积分基本定理、等比数列的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.
10.已知定义在R上的偶函数f(x),满足f(x+4)=f(x),且x∈[0,2]时,f(x)=sinπx+2|sinπx|,则方程f(x)﹣|lgx|=0在区间[0,10]上根的个数是( )
A.17 B.18 C.19 D.20
【考点】54:根的存在性及根的个数判断.
【分析】由已知写出分段函数,然后画出图象,数形结合得答案.
【解答】解:f(x)=sinπx+2|sinπx|= ,
由f(x+4)=f(x),可知f(x)是以4为周期的周期函数,
方程f(x)﹣|lgx|=0即f(x)=|lgx|,方程的根即为两函数y=f(x)与y=|lgx|图象交点的横坐标,
作出函数图象如图:
由图可知,方程f(x)﹣|lgx|=0在区间[0,10]上根的个数是19.
故选:C.
【点评】本题考查根的存在性与根的个数判断,考查数学转化思想方法与数形结合的解题思想方法,是中档题.
11.抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线 ﹣ =1(a>0,b>0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )
A. B.2 C. D. +1
【考点】KC:双曲线的简单性质.
【分析】确定抛物线y2=2px(p>0)的焦点与准线方程,利用点M为这两条曲线的一个交点,且|MF|=p,求出M的坐标,代入双曲线方程,即可求得结论.
【解答】解:抛物线y2=2px(p>0)的焦点为F( ,0),其准线方程为x=﹣ ,
∵准线经过双曲线 ﹣ =1(a>0,b>0)的左焦点,
∴c= ;
∵点M为这两条曲线的一个交点,且|MF|=p,
∴M的横坐标为 ,
代入抛物线方程,可得M的纵坐标为±p,
将M的坐标代入双曲线方程,可得 =1,
∴a= p,
∴e=1+ .
故选:D.
【点评】本题考查抛物线的几何性质,考查曲线的交点,考查双曲线的几何性质,确定M的坐标是关键.
12.已知函数f(x)=xlnx+3x﹣2,射线l:y=kx﹣k(x≥1).若射线l恒在函数y=f(x)图象的下方,则整数k的最大值为( )
A.4 B.5 C.6 D.7
【考点】6E:利用导数求闭区间上函数的最值.
【分析】由题意得问题等价于k< 对任意x>1恒成立,令g(x)= ,利用导数求得函数的最小值即可得出结论.
【解答】解:由题意,问题等价于k< 对任意x>1恒成立.
令g(x)= ,∴g′(x)= ,
令h(x)=x﹣2﹣lnx,故h(x)在(1,+∞)上是增函数,
由于h(3)=1﹣ln3<0,h(4)=2﹣ln4>0
所以存在x0∈(3,4),使得h(x0)=x0﹣2﹣lnx0=0.
则x∈(1,x0)时,h(x)<0;x∈(x0,+∞)时,h(x)>0,
即x∈(1,x0)时,g'(x)<0;x∈(x0,+∞)时,g'(x)>0
知g(x)在(1,x0)递减,(x0,+∞)递增,
又g(x0)
故选B.
【点评】本题主要考查利用导数研究函数单调性、最值等性质,考查学生的运算能力,综合性较强,属于中档题.
二、填空题(2017•广元模拟)( x﹣1)(2x﹣ )6的展开式中x的系数为 ﹣80 .(用数字作答)
【考点】DB:二项式系数的性质.
【分析】求出(2x﹣ )6展开式的常数项和含x的项,再求( x﹣1)(2x﹣ )6的展开式中x的系数.
【解答】解:(2x﹣ )6展开式的通项公式为:
Tr+1= •(2x)6﹣r• =(﹣1)r•26﹣r• •x6﹣2r,
令6﹣2r=0,解得r=3,
∴(2x﹣ )6展开式的常数项为(﹣1)3•23• =﹣160;
令6﹣2r=1,解得r= ,
∴(2x﹣ )6展开式中不含x的项;
∴( x﹣1)(2x﹣ )6的展开式中x的系数为 ×(﹣160)=﹣80.
故答案为:﹣80.
【点评】本题考查了利用二项式的通项公式求展开式特定项的应用问题,是基础题.
14.若实数x,y满足不等式组 ,则 的最小值为 3 .
【考点】7C:简单线性规划.
【分析】作出不等式组对应的平面区域,利用两点间的斜率公式进行求解即可.
【解答】解:作出不等式组对应的平面区域如图,
的几何意义是区域内的点到定点D(0,﹣1)的斜率,
由图象知BD的斜率最小,
由 得 ,即B(1,2),
此时BD的斜率k= =3,
故答案为:3
【点评】本题主要考查线性规划的应用,利用两点间的斜率公式以及数形结合是解决本题的关键.
15.在[﹣2,2]上随机抽取两个实数a,b,则事件“直线x+y=1与圆(x﹣a)2+(y﹣b)2=2相交”发生的概率为 .
【考点】CF:几何概型.
【分析】根据直线和圆相交的条件求出a,b的关系,利用线性规划求出对应区域的面积,结合几何概型的概率公式进行计算即可.
【解答】解:根据题意,得 ,
又直线x+y=1与圆(x﹣a)2+(y﹣b)2=2相交,
d≤r,
即 ≤ ,
得|a+b﹣1|≤2,
所以﹣1≤a+b≤3;
画出图形,如图所示;
则事件“直线x+y=1与圆(x﹣a)2+(y﹣b)2=2相交”发生的概率为
P= = = .
故答案为:
【点评】本题主要考查几何概型的计算,根据直线和圆相交的位置关系求出a,b的关系是解决本题的关键.注意利用数形结合以及线性规划的知识.
16.在平面内,定点A,B,C,D满足| |=| |=| |=2, • = • = • =0,动点P,M满足| |=1, = ,则| |2的最大值为 .
【考点】9R:平面向量数量积的运算.
【分析】根据题意可设D(0,0),A(2,0),B(﹣1, ),C(﹣1,﹣ ),P(2+cosθ,sinθ),M( , ),利用坐标运算求出 以及 的最大值即可.
【解答】解:平面内,| |=| |=| |=2, • = • = • =0,
∴ ⊥ , ⊥ , ⊥ ,
可设D(0,0),A(2,0),B(﹣1, ),C(﹣1,﹣ ),
∵动点P,M满足| |=1, = ,
可设P(2+cosθ,sinθ),M( , ),
∴ =( , ),
∴ = + = ≤ ,
当且仅当sin( ﹣θ)=1时取等号,
∴| |2的最大值为 .
故答案为: .
【点评】本题考查了平面向量坐标运算性质、模的计算公式、数量积运算性质以及三角函数求值问题,是综合题.
三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(12分)(2017•广元模拟)在△ABC中,a,b,c分别是角A,B,C的对边,已知3(b2+c2)=3a2+2bc.
(Ⅰ)若 ,求tanC的大小;
(Ⅱ)若a=2,△ABC的面积 ,且b>c,求b,c.
【考点】HS:余弦定理的应用.
【分析】(Ⅰ)由3(b2+c2)=3a2+2bc,利用余弦定理,可得cosA,根据 ,即可求tanC的大小;
(Ⅱ)利用面积及余弦定理,可得b、c的两个方程,即可求得结论.
【解答】解:(Ⅰ)∵3(b2+c2)=3a2+2bc,∴ =
∴cosA= ,∴sinA=
∵ ,∴
∴
∴
∴tanC= ;
(Ⅱ)∵ABC的面积 ,∴ ,∴bc= ①
∵a=2,∴由余弦定理可得4=b2+c2﹣2bc×
∴b2+c2=5②
∵b>c,∴联立①②可得b= ,c= .
【点评】本题考查余弦定理,考查三角形面积的计算,考查学生的计算能力,属于中档题.
18.(12分)(2017•广元模拟)质检部门从某超市销售的甲、乙两种食用油中分划随机抽取100桶检测某项质量指标,由检测结果得到如图的频率分布直方图:
(I)写出频率分布直方图(甲)中a的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为s12,s22,试比较s12,s22的大小(只要求写出答案);
(Ⅱ)估计在甲、乙两种食用油中随机抽取1捅,恰有一个桶的质量指标大于20,且另一个不大于20的概率;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值Z服从正态分布N(μ,δ2).其中μ近似为样本平均数 ,δ2近似为样本方差s22,设X表示从乙种食用油中随机抽取lO桶,其质量指标值位于(14.55,38.45)的桶数,求X的.散学期望.
注:①同一组数据用该区问的中点值作代表,计算得s2= ≈11.95;
②若Z﹣N(μ,δ2),则P(μ﹣δ
【考点】BC:极差、方差与标准差;B8:频率分布直方图.
【分析】(Ⅰ)按照题目要求想结果即可.
(Ⅱ)设事件A,事件B,事件C,求出P(A),P(B),P(C)即可;
(Ⅲ)求出从乙种食用油中随机抽取lO桶,其质量指标值位于(14.55,38.45)的概率是0.6826,得到X~B(10,0.6826),求出EX即可.
【解答】解:(Ⅰ)a=0.015,s12>s22;
(Ⅱ)设事件A:在甲种食用油中随机抽取1捅,其质量指标不大于20,
事件B:在乙种食用油中随机抽取1捅,其质量指标不大于20,
事件C:在甲、乙两种食用油中随机抽取1捅,恰有一个桶的质量指标大于20,且另一个不大于20,
则P(A)=0.20+0.10=0.3,P(B)=0.10+0.20=0.3,
∴P(C)=P( )P(B)+P(A)P( )=0.42;
(Ⅲ)计算得: =26.5,由条件得Z~N(26.5,142.75),
从而P(26.5﹣11.95
∴从乙种食用油中随机抽取lO桶,其质量指标值位于(14.55,38.45)的概率是0.6826,
依题意得X~B(10,0.6826),
∴EX=10×0.6826=6.826.
【点评】本题考查离散型随机变量的期望的求法,独立重复试验概率的求法,考查计算能力.
19.(12分)(2017•广元模拟)如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE= CD,M是线段AE上的动点.
(Ⅰ)试确定点M的位置,使AC∥平面DMF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
【考点】MT:二面角的平面角及求法;LS:直线与平面平行的判定.
【分析】(Ⅰ)当M是线段AE的中点时,AC∥平面DMF.连结CE,交DF于N,连结MN,利用三角形中位线定理能够证明AC∥平面DMF.
(Ⅱ)过点D作平面DMF与平面ABCD的交线l,过点M作MG⊥AD于G,过G作GH⊥l于H,连结MH,由已知条件推导出∠MHG是平面MDF与平面ABCD所成锐二面角的平面角,由此能求出所求二面角的余弦值.
【解答】解:(Ⅰ)当M是线段AE的中点时,AC∥平面DMF.
证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN⊂平面DMF,又AC不包含于平面DMF,
∴AC∥平面DMF.(4分)
(Ⅱ)过点D作平面DMF与平面ABCD的交线l,
∵AC∥平面DMF,∴AC∥l,
过点M作MG⊥AD于G,
∵平面ABCD⊥平面CDEF,DE⊥CD,
∴DE⊥平面ABCD,∴平面ADE⊥平面ABCD,
∴MG⊥平面ABCD,
过G作GH⊥l于H,连结MH,则直线l⊥平面MGH,∴l⊥MH,
∴∠MHG是平面MDF与平面ABCD所成锐二面角的平面角.(8分)
设AB=2,则DG=1,GH=DGsin∠GDH=DGsin∠DAC=1× = ,MG= =1(11分)
∴cos∠MHG= = ,
∴所求二面角的余弦值为 .(12分)
【点评】本题考查直线与平面平行的判定及证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.
20.(12分)(2017•广元模拟)已知△ABC中,角A,B,C所对的边分别是a,b,c,且点A(﹣1,0),B(1,0),动点C满足 =λ(λ为常数且λ>1),动点C的轨迹为曲线E.
(Ⅰ)试求曲线E的方程;
(Ⅱ)当λ= 时,过定点B(1,0)的直线与曲线E交于P,Q两点,N是曲线E上不同于P,Q的动点,试求△NPQ面积的最大值.
【考点】KL:直线与椭圆的位置关系.
【分析】(Ⅰ)由题意可知丨CA丨+丨CB丨=2λ>2,则动点C的轨迹P为椭圆(除去A、B与共线的两个点).即可求得求曲线E的方程;
(Ⅱ)当λ= 时,求得椭圆方程,分类讨论,设直线l的方程,代入椭圆方程,利用韦达定理,弦长公式及点到直线的距离公式,利用导数求得函数单调性区间,即可求得△NPQ面积的最大值.
【解答】解:(Ⅰ)在△ABC中,由丨AB丨=2,则丨CA丨+丨CB丨=2λ(定值),且2λ>2,
∴动点C的轨迹P为椭圆(除去A、B与共线的两个点).
设其标准方程为 (a>b>0),则a2﹣λ2b2﹣λ2=1,
∴求曲线的轨迹方程为 (x≠±λ),
(Ⅱ)当λ= 时,椭圆方程为 (x≠± ),.
①过定点B的直线与x轴重合时,△NPQ面积无最大值,
②过定点B的直线不与x轴重合时,
设l方程为:x=my+1,P(x1,y1)、Q(x2,y2),
若m=0,由x≠± ,故此时△NPQ面积无最大值.
根据椭圆的几何性质,不妨设m>0,
联立方程组 ,消去x整理得:(3+2m2)y2+4my﹣4=0,
∴y1+y2=﹣ ,y1y2=﹣ ,则丨PQ丨= 丨y1﹣y2丨= .
因为当直线l与平行且与椭圆相切时,切点N到直线l的距离最大,
设切线l:x=my+n(n< ),
联立 ,消去x整理得(3+2m2)y2+4mny+2n2﹣6=0,
由△=(4mn)2﹣4(3+2m2)(2n2﹣6)=0,解得:2n2﹣3+2m2=0,n<﹣ .
又点N到直线l的距离d= ,
∴△NPQ面积S= 丨PQ丨d= × × = ,
∴S2= .将n2=3+2m2,代入得:S2=6(1﹣ )2(1﹣( )2),
令t= ∈(﹣ ,0),设函数f(t)=6(1﹣t)2(1﹣t2),则f′(t)=﹣12(t﹣1)2(2t+1),
由当t∈(﹣ ,﹣ )时,f′(t)>0,当t∈(﹣ ,0)时,f′(t)<0,
∴f(t)在(﹣ ,﹣ )上是增函数,在(﹣ ,0)上是减函数,
∴fmin(t)=f(﹣ )= .
故m2= 时,△NPQ面积最大值是 .
∴当l的方程为x=± y+1时,△NPQ的面积最大,最大值为 .
【点评】本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,三角形的面积公式,考查利用导数求函数的单调性及最值,考查计算能力,属于中档题.
21.(12分)(2017•广元模拟)已知函数f(x)=exsinx﹣cosx,g(x)=xcosx﹣ ex,其中e是自然对数的底数.
(1)判断函数y=f(x)在(0, )内的零点的个数,并说明理由;
(2)∀x1∈[0, ],∃x2∈[0, ],使得f(x1)+g(x2)≥m成立,试求实数m的取值范围;
(3)若x>﹣1,求证:f(x)﹣g(x)>0.
【考点】6B:利用导数研究函数的单调性;52:函数零点的判定定理;63:导数的运算.
【分析】(1)利用导数得到函数y=f(x)在(0, )上单调递增,f(0)=﹣1<0,f( )>0,根据函数零点存在性定理得函数y=f(x)在(0, )内的零点的个数为1;
(2)确定函数f(x)在[0, ]上单调递增,可得f(x)min=f(0)=﹣1;函数g(x)在[0, ]上单调递减,可得g(x)max=g(0)=﹣ ,即可求出实数m的范围;
(3)先利用分析要证原不等式成立,转化为只要证 > ,令h(x)= ,x>﹣1,利用导数求出h(x)min=h(0)=1,再令k= ,其可看作点A(sinx,cosx)与点B(﹣ ,0)连线的斜率,根据其几何意义求出k的最大值,即可证明.
【解答】解:(1)函数y=f(x)在(0, )内的零点的个数为1,
理由如下:∵f(x)=exsinx﹣cosx,
∴f′(x)=ex(sinx+cosx)+sinx,
∵x∈(0, ),
∴f′(x)>0,
∴函数y=f(x)在(0, )上单调递增,
∵f(0)=﹣1<0,f( )>0,
根据函数零点存在性定理得函数y=f(x)在(0, )内的零点的个数为1.
(2)∵f(x1)+g(x2)≥m,
∴f(x1)≥m﹣g(x2),
∴f(x1)min≥[m﹣g(x2)]min,
∴f(x1)min≥m﹣g(x2)max,
当x∈[0, ]时,f′(x)>0,函数f(x)在[0, ]上单调递增,
∴f(x)min≥f(0)=﹣1,
∵g(x)=xcosx﹣ ex,
∴g′(x)=cosx﹣xsinx﹣ ex,
∵x∈[0, ],
∴0≤cosx≤1,xsinx≥0, ex≥ ,
∴g′(x)≤0,
∴函数g(x)在[0, ]上单调递减,
∴g(x)max≥g(0)= ,
∴﹣1≥m+ ,
∴m≤﹣1﹣ ,
∴实数m的取值范围为(﹣∞,﹣1﹣ ];
(3)x>﹣1,要证:f(x)﹣g(x)>0,
只要证f(x)>g(x),
只要证exsinx﹣cosx>xcosx﹣ ex,
只要证ex(sinx+ )>(x+1)cosx,
由于sinx+ >0,x+1>0,
只要证 > ,
下面证明x>﹣1时,不等式 > 成立,
令h(x)= ,x>﹣1,
∴h′(x)= ,x>﹣1,
当x∈(﹣1,0)时,h′(x)<0,h(x)单调递减,
当x∈(0,+∞)时,h′(x)>0,h(x)单调递增,
∴h(x)min=h(0)=1
令k= ,其可看作点A(sinx,cosx)与点B(﹣ ,0)连线的斜率,
∴直线AB的方程为y=k(x+ ),
由于点A在圆x2+y2=1上,
∴直线AB与圆相交或相切,
当直线AB与圆相切且切点在第二象限时,直线AB的斜率取得最大值为1,
∴当x=0时,k= <1=h(0),x≠0时,h(x)>1≥k,
综上所述,当x>﹣1,f(x)﹣g(x)>0.
【点评】本题考查了函数零点存在性定理,导数和函数的最值的关系,以及切线方程,考查分类整合思想、转化思想,考查学生综合运用知识分析解决问题的能力.注意认真体会(3)问中几何中切线的应用,属于难题.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.(10分)(2017•广元模拟)在平面直角坐标系xOy中,曲线C1: (α是参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2:ρcosθ﹣3=0.点P是曲线C1上的动点.
(1)求点P到曲线C2的距离的最大值;
(2)若曲线C3:θ= 交曲线C1于A,B两点,求△ABC1的面积.
【考点】Q4:简单曲线的极坐标方程.
【分析】(1)求得C1的标准方程,及曲线C2的标准方程,则圆心C1到x=3距离d,点P到曲线C2的距离的最大值dmax=R+d=6;
(2)将直线l的方程代入C1的方程,求得A和B点坐标,求得丨AB丨,利用点到直线的距离公式,求得C1到AB的距离d,即可求得△ABC1的面积.
【解答】解(1)曲线C1: (α是参数).整理得:(x+2)2+(y+1)2=1
曲线C2:ρcosθ﹣3=0,则x=3.
则圆心C1到x=3距离d,d=2+3=5,
点P到曲线C2的距离的最大值dmax=R+d=6;
∴点P到曲线C2的距离的最大值6;
(2)若曲线C3:θ= ,即y=x,
,解得: , ,
丨AB丨= =
∴C1到AB的距离d= = ,
则△ABC1的面积S,S= × × = .
∴△ABC1的面积 .
【点评】本题考查参数方程与普通方程的转化,直线与的圆的位置关系,考查点到直线的距离公式,属于中档题.
[选修4-5:不等式选讲]
23.(2013•辽宁)已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
【考点】&2:带绝对值的函数;R5:绝对值不等式的解法.
【分析】(1)当a=2时,f(x)≥4﹣|x﹣4|可化为|x﹣2|+|x﹣4|≥4,直接求出不等式|x﹣2|+|x﹣4|≥4的解集即可.
(2)设h(x)=f(2x+a)﹣2f(x),则h(x)= .由|h(x)|≤2解得 ,它与1≤x≤2等价,然后求出a的值.
【解答】解:(1)当a=2时,f(x)≥4﹣|x﹣4|可化为|x﹣2|+|x﹣4|≥4,
当x≤2时,得﹣2x+6≥4,解得x≤1;
当2
当x≥4时,得2x﹣6≥4,解得x≥5;
故不等式的解集为{x|x≥5或x≤1}.
(2)设h(x)=f(2x+a)﹣2f(x),则h(x)=
由|h(x)|≤2得 ,
又已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},
所以 ,
故a=3.
【点评】本题是中档题,考查绝对值不等式的解法,注意分类讨论思想的应用,考查计算能力,常考题型.
【届淄博市高考理科数学模拟试卷及答案】相关文章:
2018届广西高考理科数学模拟试卷及答案12-11
2018届青冈高考理科数学模拟试卷及答案12-11